What Is The Surface Area Of The Right Triangular Prism Show Your Work The total surface area of a triangular prism is the sum of the areas of all its faces the three lateral faces rectangles and two bases triangles The most general formula for the surface area of any prism is Total area Lateral area 2 215 Base area
May 14 2018 nbsp 0183 32 To find the surface area of a triangular prism we need to sum the areas of all its faces A triangular prism has two triangular bases and three rectangular lateral faces Calculate the area of the triangular bases The area of one triangle can be Mar 15 2022 nbsp 0183 32 To find the surface area of a right triangular prism we can use the formula Surface Area Perimeter of the triangular base 215 length of the prism 2 215 Area of the triangular base Calculate the Perimeter of the Triangular Base If we assume the sides of the triangle are given as S1 S2 and S3
What Is The Surface Area Of The Right Triangular Prism Show Your Work

What Is The Surface Area Of The Right Triangular Prism Show Your Work
https://us-static.z-dn.net/files/d79/60d78b4f9962c924ff584a22787d1ceb.jpg

Question Video Finding The Volume Of A Triangular Prism Nagwa
https://media.nagwa.com/597151459369/en/thumbnail_l.jpeg
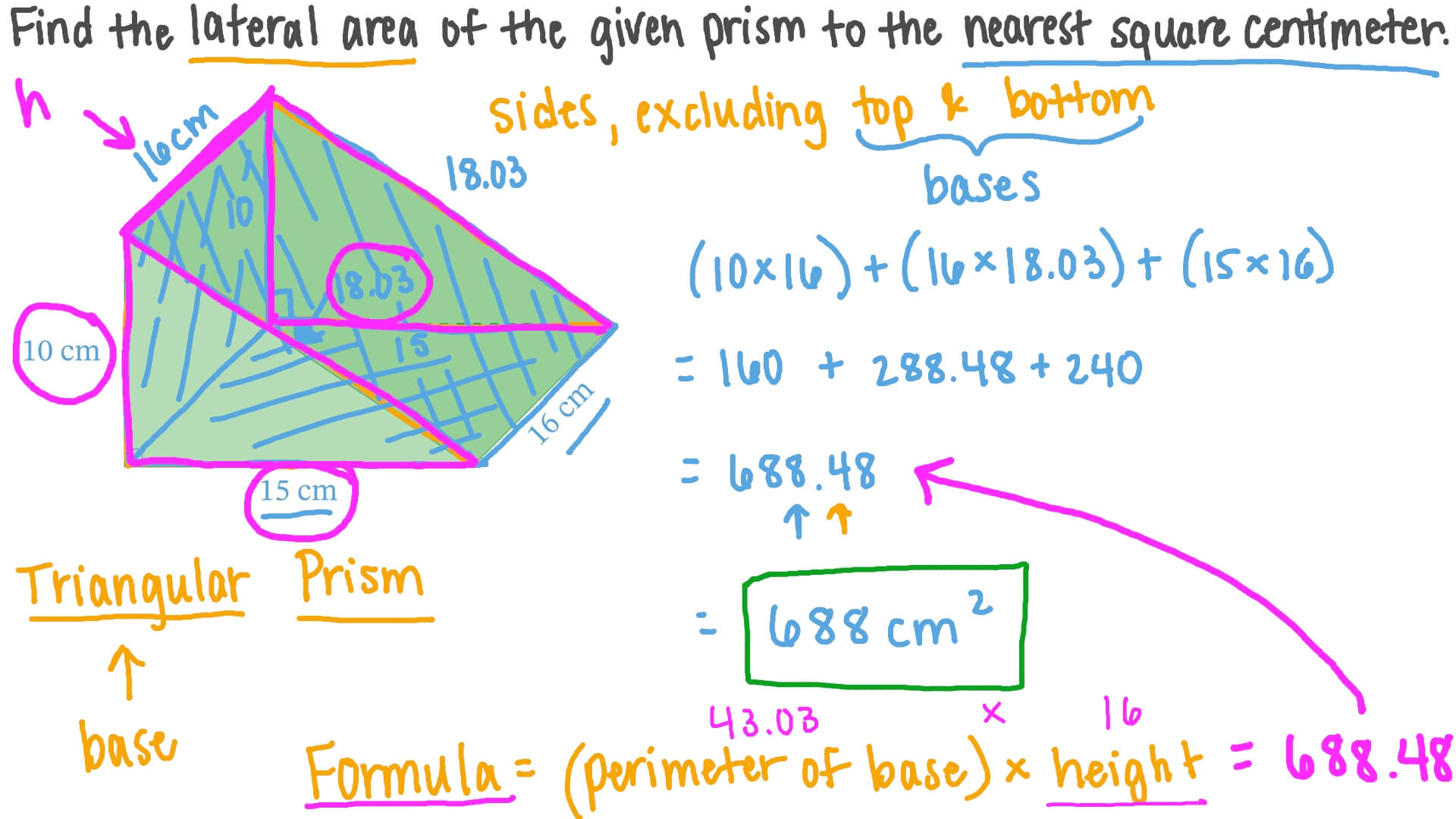
Question Video Finding The Lateral Surface Area Of A Triangular Prism
https://media.nagwa.com/128105275726/en/thumbnail_l.jpeg
What is the surface area of a triangular prism The surface area of a triangular prism is the total area of all of the faces of the triangular prism To calculate the surface area of triangular prisms you need to calculate the area of each face and add them all together Surface area of triangular prism is the total area covered by its surface in three dimensional plane The formula is given by Surface area bh a b c H Where a b and c are the sides of triangular bases and H is the height of the prism
Oct 4 2023 nbsp 0183 32 This calculator finds the volume surface area and height of a triangular prism Surface area calculations include top bottom lateral sides and total surface area Height is calculated from known volume or lateral surface area Jul 29 2024 nbsp 0183 32 Let s check what s the volume and surface area of a tent shaped like a triangular prism Find out what s the length of the triangular prism Assume it s equal to 80 in type this value into the first box of the triangular prism calculator
More picture related to What Is The Surface Area Of The Right Triangular Prism Show Your Work

Question Video Finding The Surface Area Of Right Triangular Prisms Nagwa
https://media.nagwa.com/527180620571/en/thumbnail_l.jpeg

Area For Triangular Prism
https://us-static.z-dn.net/files/d2c/9c2264bb18170c24758f5f2657076014.png
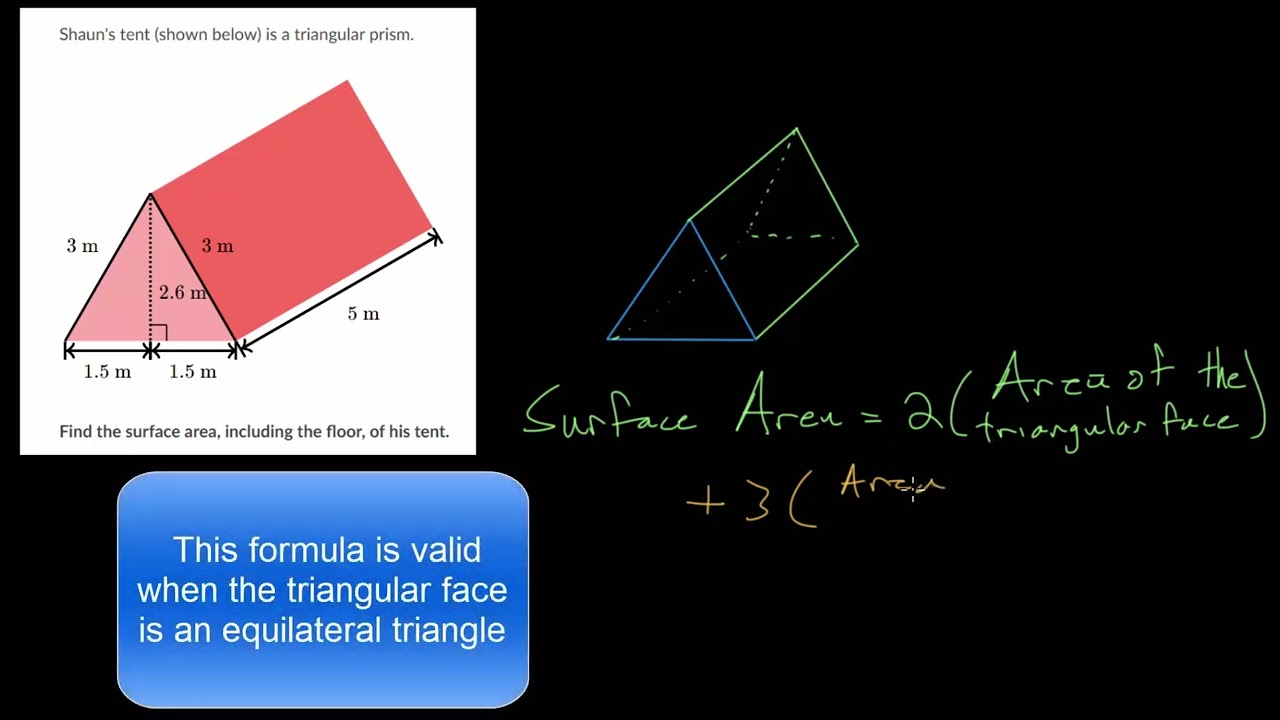
Surface Area Equilateral Triangular Prism YouTube
https://i.ytimg.com/vi/YYqbdI49ojg/maxresdefault.jpg
Aug 3 2023 nbsp 0183 32 Learn how to find the surface area of a triangular prism explained with formulas solved examples and diagrams What is the surface area of a triangular prism The surface area of a triangular prism is the total area of all of the faces To work out the surface area of a triangular prism we need to work out the area of each face and add them all together
Calculate the total surface area of the triangular prism Image caption The total surface area of the prism is made up of two congruent triangles and three differently sized rectangles The formula to calculate the surface area of a triangular prism is as follows Surface Area bh s1 s2 s3 l Where b is the area of the base h is the height of the triangle s1 s2 and s3 are the sides of the triangle and l is the length of the prism
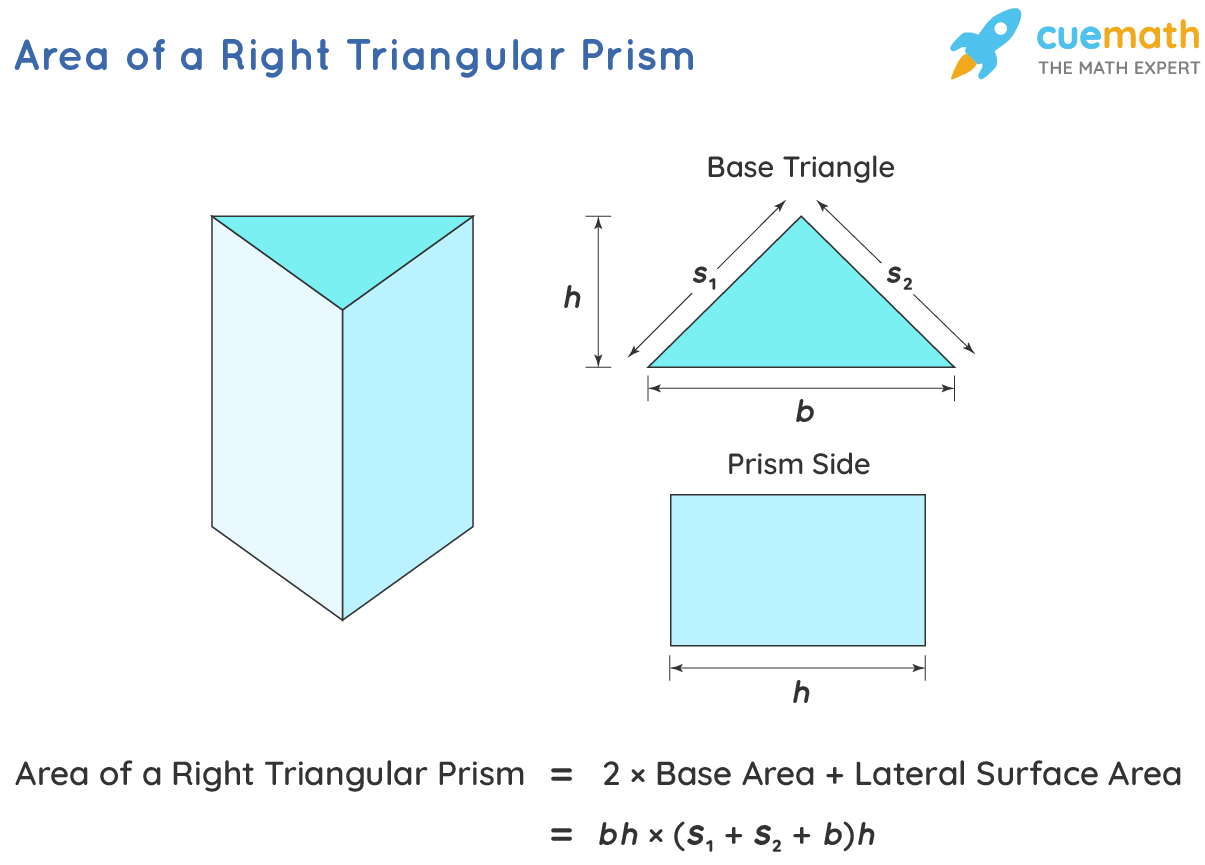
Surface Area Of A Triangular Prism Formula Examples Definition
https://d138zd1ktt9iqe.cloudfront.net/media/seo_landing_files/area-of-a-right-triangular-prism-1621771213.png

Area Of Triangular Prism Formula Slideshare
https://i.ytimg.com/vi/HtXPpqKud5U/maxresdefault.jpg
What Is The Surface Area Of The Right Triangular Prism Show Your Work - Jul 29 2024 nbsp 0183 32 Let s check what s the volume and surface area of a tent shaped like a triangular prism Find out what s the length of the triangular prism Assume it s equal to 80 in type this value into the first box of the triangular prism calculator