Non Terminating Decimal To Fraction Non terminating decimals are decimals that have never ending decimal digits and continue forever We will be learning about the non terminating decimal expansion and conversion of non terminating decimal to fraction in this article
In this article we are going to discuss how to convert repeating decimals to fractions in an easy way Terminating and Non Terminating Decimals A terminating decimal is a decimal that has an end digit It is a decimal which has a finite number of digits or terms Example 0 15 0 86 etc Jan 16 2017 nbsp 0183 32 Learn how to convert a non terminating decimal also called a repeating decimal into a fraction Please watch quot Study Skills Teacher s Secret G
Non Terminating Decimal To Fraction

Non Terminating Decimal To Fraction
https://i.ytimg.com/vi/d_2j__FsS88/maxresdefault.jpg

Converting Repeating Decimals To Fractions YouTube
https://i.ytimg.com/vi/mvtHSh4PQxo/maxresdefault.jpg

Terminating And Repeating Decimals Worksheet
https://d1e4pidl3fu268.cloudfront.net/12623a58-3375-4977-aeab-1be087383ab2/Clickerscreen.png
It is very easy to convert a terminating decimal to a fraction but how do we convert a repeating decimal to fraction Repeating decimals are decimal numbers that do not terminate after a finite number of digits and in these numbers one or more digits repeat themselves again and again Rational numbers when written as decimals are either terminating or non terminating repeating decimals Converting terminating decimals into fractions is straightforward multiplying and dividing by an appropriate power of ten does the trick For example 2 556753 frac 2556753 1000000
Mar 6 2024 nbsp 0183 32 In this tutorial we will learn about non terminating repeating decimals and how to convert them to fractions A number separating an integral part and the fractional part by a point is called a decimal number or decimal The separating point is called the decimal point Jun 1 2023 nbsp 0183 32 What is a Non Terminating Decimal A non terminating decimal is a decimal number that goes on forever without reaching an end or settling into a repeating pattern It is a number that cannot be expressed as a fraction with finite digits
More picture related to Non Terminating Decimal To Fraction

Trick To Convert Non Terminating Repeating Decimals Into Fractions
https://i.ytimg.com/vi/JAFNrHCPKC4/maxresdefault.jpg

Non terminating Decimal To Fraction YouTube
https://i.ytimg.com/vi/ONJo8jNWaCM/maxresdefault.jpg

ShowMe Terminating Decimals
https://showme1-9071.kxcdn.com/2020/09/29/12/OG68T1k_ShowMe_last_thumb.jpg
Follow these steps to use recurring decimals to fractions calculator for the conversion of non terminating decimals Enter a recurring number in the next input box Enter the non recurring part optional in the given input box Hit the Calculate button to get the fraction Use the Reset button to enter new values In this article we are going to discuss how to convert repeating decimals to fractions in an easy way A terminating decimal is a decimal that has an end digit It is a decimal which has a finite number of digits or terms Example 0 15 0 86 etc Non terminating decimals are the one that does not have an end term
[desc-10] [desc-11]
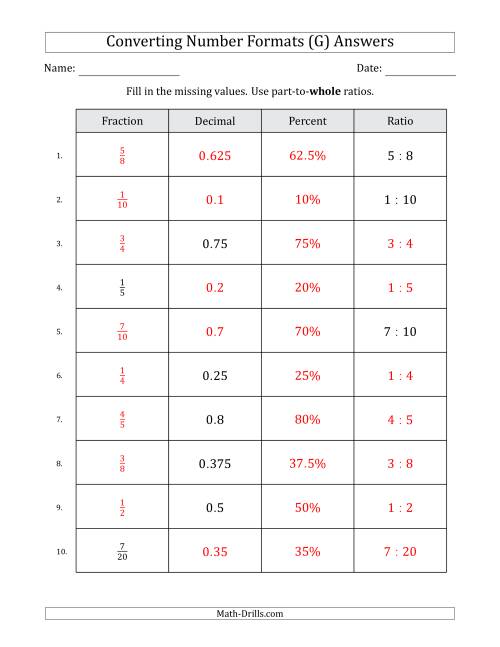
Converting Between Fractions Decimals Percents And Part to Whole
https://www.math-drills.com/fractions/images/convert_fractions_terminating_from_various_to_various_pwratios_007_pin2.1562347584.jpg

Converting Terminating And Repeating Decimals To Fractions A
https://www.math-drills.com/decimal/images/decimals_convert_to_fractions_001_pin2.jpg?v=1479311840
Non Terminating Decimal To Fraction - Jun 1 2023 nbsp 0183 32 What is a Non Terminating Decimal A non terminating decimal is a decimal number that goes on forever without reaching an end or settling into a repeating pattern It is a number that cannot be expressed as a fraction with finite digits