How To Find The Perimeter Of A Regular Polygon With Apothem Jun 22 2022 nbsp 0183 32 Given the number of sides n and the length of side s of a regular polygon the task is to find out the Perimeter of this polygon Examples Input n 7 s 10 Output
The apothem of a regular polygon is a line segment from the center of the polygon perpendicular to any side of the polygon With a series of substitutions we can arrive at a formula A polygon having equal sides and equal angles is a regular polygon To find area of regular polygon we use the formula Area of regular polygon 1 2 215 Perimeter 215 Apothem
How To Find The Perimeter Of A Regular Polygon With Apothem
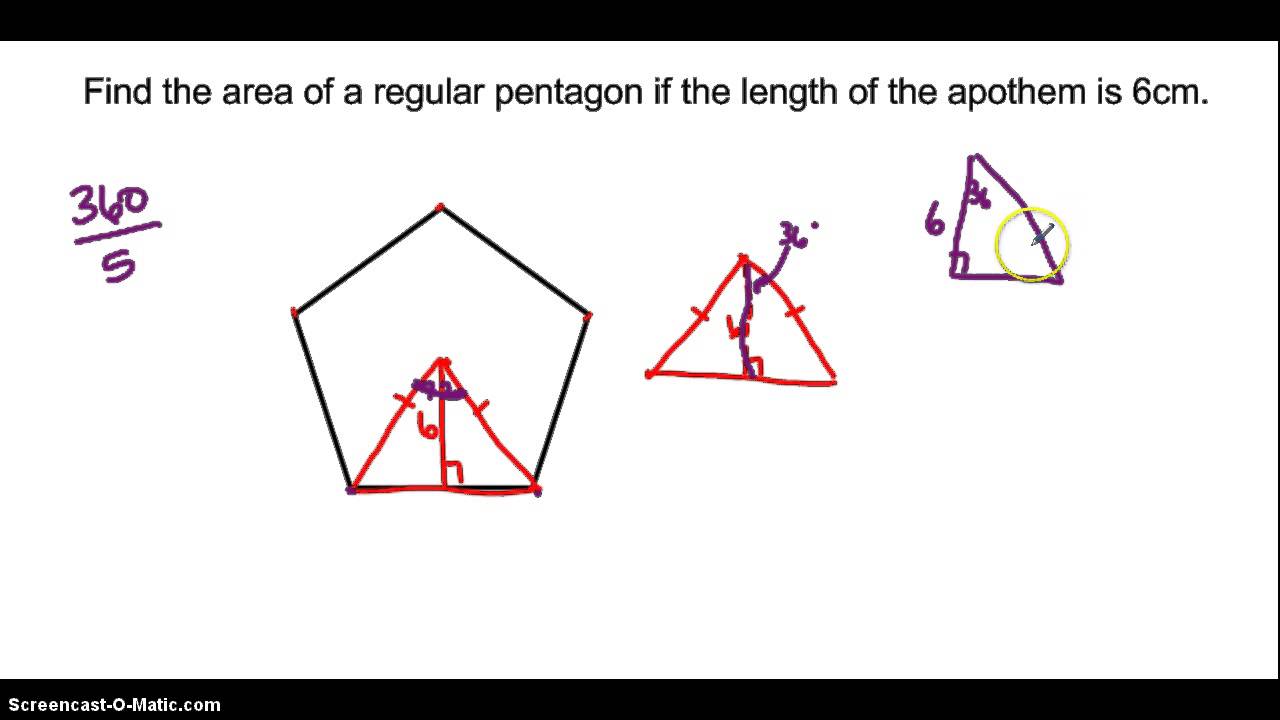
How To Find The Perimeter Of A Regular Polygon With Apothem
https://i.ytimg.com/vi/qYV-cOV97ns/maxresdefault.jpg

Derivation Of Formula For Area Of Regular Polygons With Side And
https://i.ytimg.com/vi/cFO76DjXMw8/maxresdefault.jpg
G17a Perimeter Of Polygons BossMaths
https://bossmaths.com/wp-content/uploads/G17as.001.png
Each formula below shows how to find the length of the apothem of a regular polygon Use the formula that uses the facts you are given to start Apothem given the length of a side By Nov 21 2023 nbsp 0183 32 How do you find the apothem The apothem is the segment length from the center of a regular polygon to the midpoint of any of its sides It can be calculated using formulas that
Use our free Regular Polygon Calculator to instantly compute side length inradius circumradius area perimeter and angles for any regular polygon Perfect for geometry students and Area 0 5 x apothem x perimeter For a regular polygon the apothem is the distance from the center of the polygon to the midpoint of one of its sides The perimeter is the sum of the lengths
More picture related to How To Find The Perimeter Of A Regular Polygon With Apothem
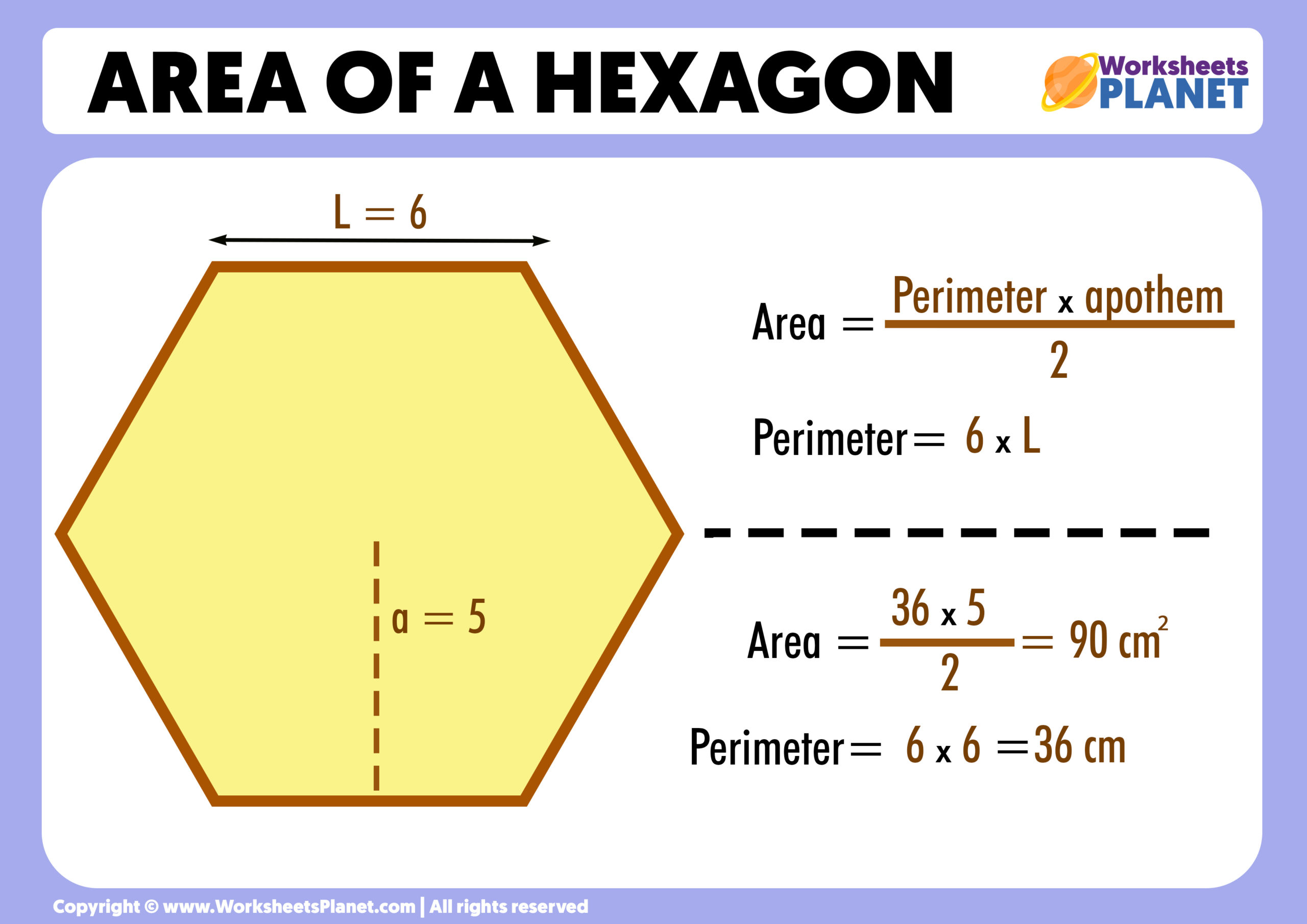
Area Of A Hexagon Formula Example
https://www.worksheetsplanet.com/wp-content/uploads/2022/09/Area-of-a-hexagon-scaled.jpg

Objectives Develop And Apply The Formula For The Area Of A Regular
https://slideplayer.com/slide/12901919/78/images/4/To+find+the+area+of+a+regular+n-gon+with+side+length+s+and+apothem+a%2C+divide+it+into+n+congruent+isosceles+triangles..jpg

Objectives Develop And Apply The Formula For The Area Of A Regular
https://slideplayer.com/slide/12901919/78/images/12/Example+3B+Continued+Step+3+Use+the+apothem+and+the+given+side+length+to+find+the+area.+Area+of+a+regular+polygon..jpg
Enter the length of any side and total number of sides of the polygon into the calculator to determine the apothem Mar 15 2025 nbsp 0183 32 Perimeter The perimeter of a polygon is calculated as the number of sides multiplied by the side length Area The area of a regular polygon is calculated using the
To calculate the perimeter of a regular polygon simply multiply the number of sides n times the side length a perimeter n 215 a If you want to determine the perimeter of any polygon sum Aug 3 2023 nbsp 0183 32 All sides of a regular polygon being equal in length we can obtain its perimeter by repeated addition of each of its side The perimeter of a regular polygon with n sides can be

The Interior Angle Of A Convex Regular Polygon Is 4 Times The Exterior
https://hi-static.z-dn.net/files/d53/b545ac25cabda3846813dd6d5094d24b.jpg
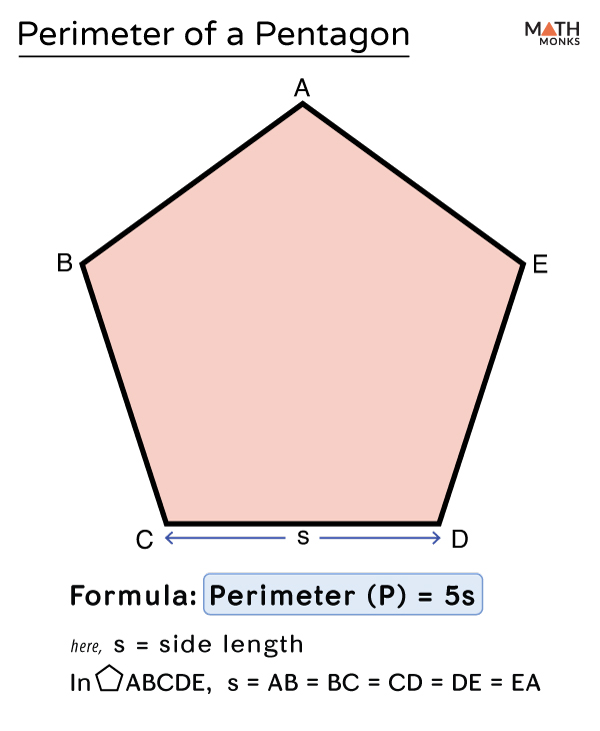
Perimeter Of Pentagon Formulas Examples And Diagrams
https://mathmonks.com/wp-content/uploads/2021/11/Perimeter-of-Pentagon.jpg
How To Find The Perimeter Of A Regular Polygon With Apothem - Mar 13 2018 nbsp 0183 32 Divide the result from Step 3 by the perimeter found in Step 2 to calculate the apothem Concluding this example you would divide 254 62 by 42 to find the length of the