Volume Between Curves Formula Nov 16 2022 nbsp 0183 32 To get a solid of revolution we start out with a function y f x y f x on an interval a b a b We then rotate this curve about a given axis to get the surface of the solid of revolution For purposes of this discussion let s rotate the curve about the x x axis although it could be any vertical or horizontal axis
Nov 4 2021 nbsp 0183 32 Just as we can use definite integrals to add the areas of rectangular slices to find the exact area that lies between two curves we can also employ integrals to determine the volume of certain regions that have cross sections of a particular consistent shape Now imagine that a curve for example y x 2 is rotated around the x axis so that a solid is formed The volume of the shape that is formed can be found using the formula Rotation about the y axis If the body is rotated about the y axis rather than the x axis then we use the formula
Volume Between Curves Formula
Volume Between Curves Formula
https://i.ytimg.com/vi/DlUjqdHvuNk/maxresdefault.jpg?sqp=-oaymwEmCIAKENAF8quKqQMa8AEB-AH-CYAC0AWKAgwIABABGHIgQChCMA8=&rs=AOn4CLC-4QKpi6UDTrxxIG3hSUPfW10wRQ
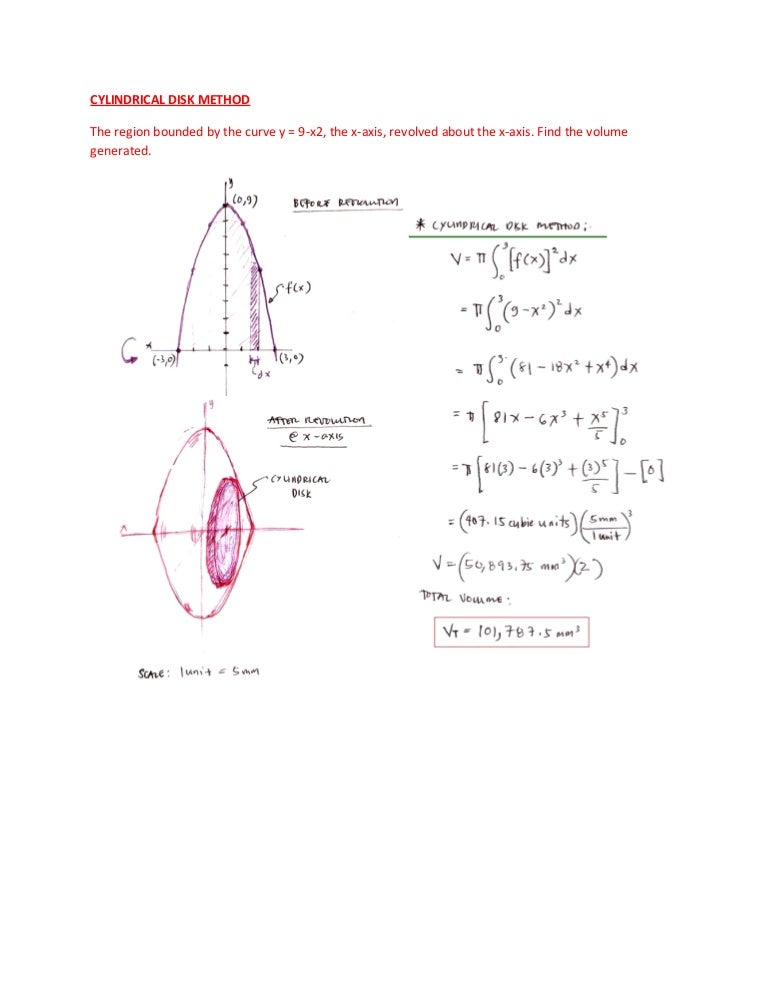
Volume Of Curves Revolved About An Axis Using Integration
https://cdn.slidesharecdn.com/ss_thumbnails/volumeofcurvesrevolvedaboutanaxisusingintegration-121024055246-phpapp01-thumbnail-4.jpg?cb=1351058008
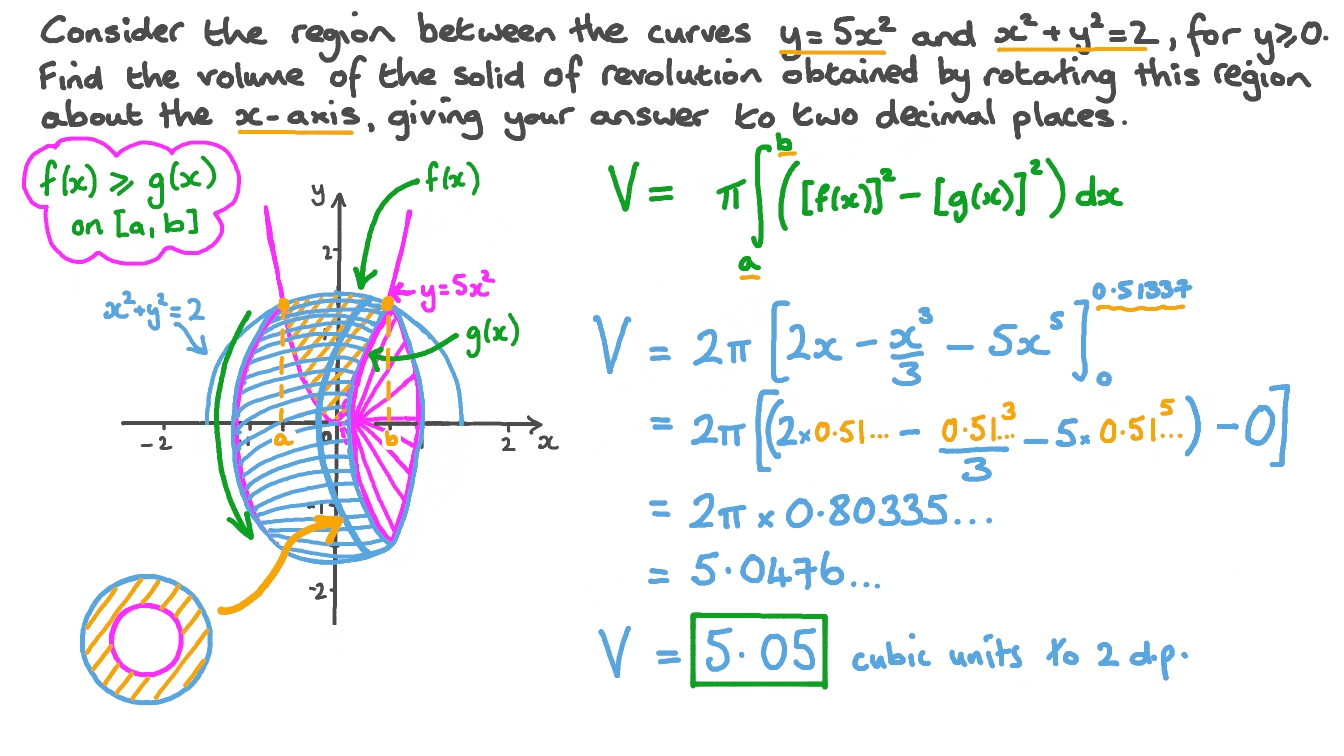
Question Video Finding The Volume Of A Solid Of Revolution Bounded By
https://media.nagwa.com/127174023949/en/thumbnail_l.jpeg
Calculate volumes of revolved solid between the curves the limits and the axis of rotation Jan 8 2019 nbsp 0183 32 To find the volume between the curves you will integrate the difference of the two functions over the interval a b a b The formula is V b a f x g x dx V a b f x g x d x Calculate the definite integral of the difference between the two functions from a a to b b
One very useful application of Integration is finding the area and volume of curved figures that we couldn t typically get without using Calculus Since we already know that can use the integral to get the area between the x and y axis and a function we can also get the volume of this figure by rotating the figure around either Find the volume of a solid of revolution obtained from a simple function y f x where the limits are obtained from the geometry of the solid 1 Introduction Suppose we have a curve y f x x axis through 360 The curve would then map out the surface of a solid as it rotated Such solids are called solids of revolution
More picture related to Volume Between Curves Formula
Calculus Calculating A Rotation Volume Rotating Around y 1
https://i.stack.imgur.com/KrYgt.jpg
The Washer Method YouTube
https://i.ytimg.com/vi/KI5Nfynu0F8/maxresdefault.jpg?sqp=-oaymwEmCIAKENAF8quKqQMa8AEB-AHUBoAC4AOKAgwIABABGGogaihqMA8=&rs=AOn4CLAp9C4vNfUFGPfWN1tJ1ZSmGgTY2Q
Estimating The Volume Formed By The Intersection Of Two Curves Using
https://i.ytimg.com/vi/kLb55RFHkEY/maxresdefault.jpg
In this section the second of two sections devoted to finding the volume of a solid of revolution we will look at the method of cylinders shells to find the volume of the object we get by rotating a region bounded by two curves one of which may be the x or y The washer method is an extension of the disk method and allows us to find the solid s volume formed by two curves Master this topic here
[desc-10] [desc-11]
Volume Of Revolution About The X axis Between Curves 2
https://i.ytimg.com/vi/E0JJ_tgl59o/maxresdefault.jpg
Disk Washer Method Calculus Membership YouTube
https://i.ytimg.com/vi/7CMTMCS0Zq0/maxresdefault.jpg
Volume Between Curves Formula - Find the volume of a solid of revolution obtained from a simple function y f x where the limits are obtained from the geometry of the solid 1 Introduction Suppose we have a curve y f x x axis through 360 The curve would then map out the surface of a solid as it rotated Such solids are called solids of revolution