Geometry Medians And Altitudes Of Triangles Worksheet Answers Use medians and fi nd the centroids of triangles Use altitudes and fi nd the orthocenters of triangles Using the Median of a Triangle A median of a triangle is a segment from a vertex to the midpoint of the opposite side The three medians of a triangle are concurrent The point of concurrency called the centroid is inside the triangle
Name all the parts in the triangle Median Angle Bisector Altitude Perpendicular Bisector If E is the midpoint of AB F is the midpoint of BC and G is the midpoint of AC Name each The altitudes of ABC The medians of ABC Underline the correct word or These worksheets can be used to learn and practice finding the altitude and median of a triangle This will also help you better understand the concept of the area of a triangle by drawing its altitude and then using the base x altitude formula
Geometry Medians And Altitudes Of Triangles Worksheet Answers

Geometry Medians And Altitudes Of Triangles Worksheet Answers
https://i.ytimg.com/vi/K4vwZoiAizo/maxresdefault.jpg

LESSON 5 3 PROBLEM SOLVING MEDIANS AND ALTITUDES OF TRIANGLES
https://i.ytimg.com/vi/RNdGwmJiT_M/maxresdefault.jpg

Two Column Proofs Triangles Medians And Altitudes YouTube
https://i.ytimg.com/vi/ZJ_gqFidInk/maxresdefault.jpg
Draw using a straightedge and label a figure to illustrate each situation 11 OQ is a median and an altitude of POM 12 KT is an altitude of KLM and L is between T and M 13 HS is an angle bisector of GHI and S is between G and I 14 Kuta Software Infinite Geometry Name Medians Date Period Each figure shows a triangle with one or more of its medians 1 Find FE if TE 8 F T E G 16 2 Find GF if TF 6 3 T E F G 12 6 3 Find LJ if IJ 6 N L J K I 3 4 Find NM if EM 10 E L M N 20 5 Find ZQ if ZD 6 F D Y Z X Q 4 6 Find RK if DK 3 4 K I T R S D 10 2
MEDIANS AND ALTITUDES OF A TRIANGLE WORKSHEET Problem 1 Construct the centroid of ABC whose sides are AB 6cm BC 7cm and AC 5cm Problem 2 Construct ABC whose sides are AB 6cm BC 4cm and AC 5 5cm and locate its orthocenter Problem 3 I can use the median point of concurrency the centroid to find segment lengths In STR H is the centroid EH 6 DH 4 and SM 24 Find each length
More picture related to Geometry Medians And Altitudes Of Triangles Worksheet Answers
Finding Angles And Sides Of A Triangle With Altitude Worksheet
https://www.angleworksheets.com/wp-content/uploads/2022/10/medians-and-altitudes-of-triangles-worksheet-worksheet.png

Median Altitude Geometry Killerxoler
https://i.ytimg.com/vi/Jy2ZEhweZVk/maxresdefault.jpg

Medians And Altitudes Of Triangles Worksheet Answers
https://i2.wp.com/pvphsgarnet.weebly.com/uploads/3/7/3/2/3732843/20141120_05-3_hw2.jpg
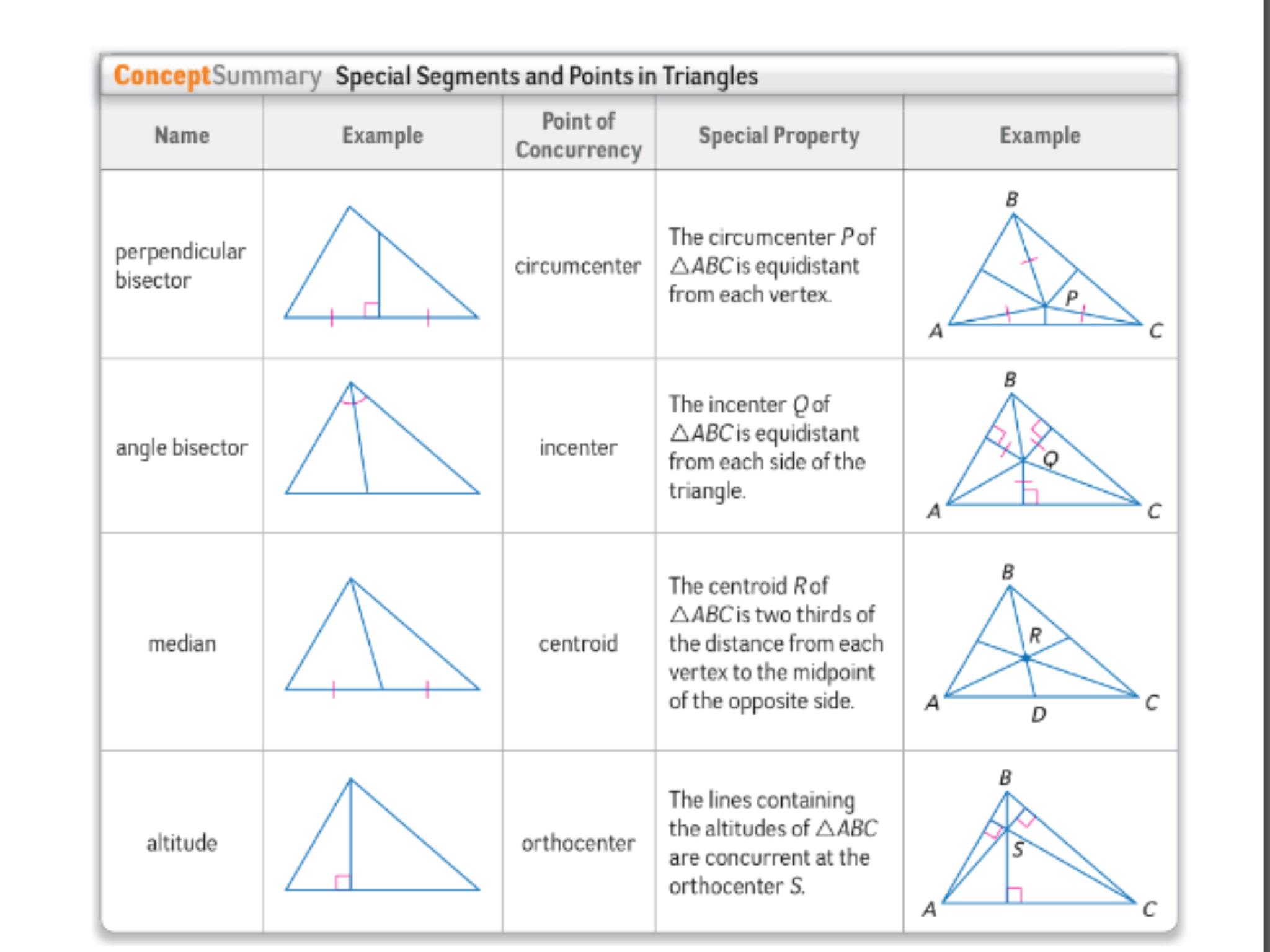
Altitudes of the triangle rather than the medians An altitude of a triangle is a perpendicular segment from a vertex to the line containing the opposite side O Triangle 1 Three perpendicular bisectors one on each side of the triangle Label the point where they intersect Circumcenter o Triangle 2 Three angle bisectors one from each angle in the triangle Label the point where they intersect Incenter o Triangle 3 Three medians one on each side of the triangle
The medians of a triangle intersect at a point that is two thirds of the distance from each vertex to the midpoint of the opposite side This point is called the centroid and is the center of balance of the triangle BP 2 A median of a triangle is a segment whose endpoints are a vertex of the triangle and the midpoint of the opposite side Every triangle has three medians and the medians are concurrent The point of concurrency of the medians of a triangle is the centroid of the triangle The centroid is always inside the triangle

Angle Bisectors Medians And Altitudes YouTube Worksheets Library
https://worksheets.clipart-library.com/images2/angle-bisector-median-altitude-perpendicular-bisector/angle-bisector-median-altitude-perpendicular-bisector-5.jpg
Medians And Altitudes In Triangles CK 12 Foundation
https://dr282zn36sxxg.cloudfront.net/datastreams/f-d%3A85a93598a712792b7a4f3efe51240cb43ab0068b7036e7fb2ff19cd3%2BIMAGE%2BIMAGE.1
Geometry Medians And Altitudes Of Triangles Worksheet Answers - Draw using a straightedge and label a figure to illustrate each situation 11 OQ is a median and an altitude of POM 12 KT is an altitude of KLM and L is between T and M 13 HS is an angle bisector of GHI and S is between G and I 14
